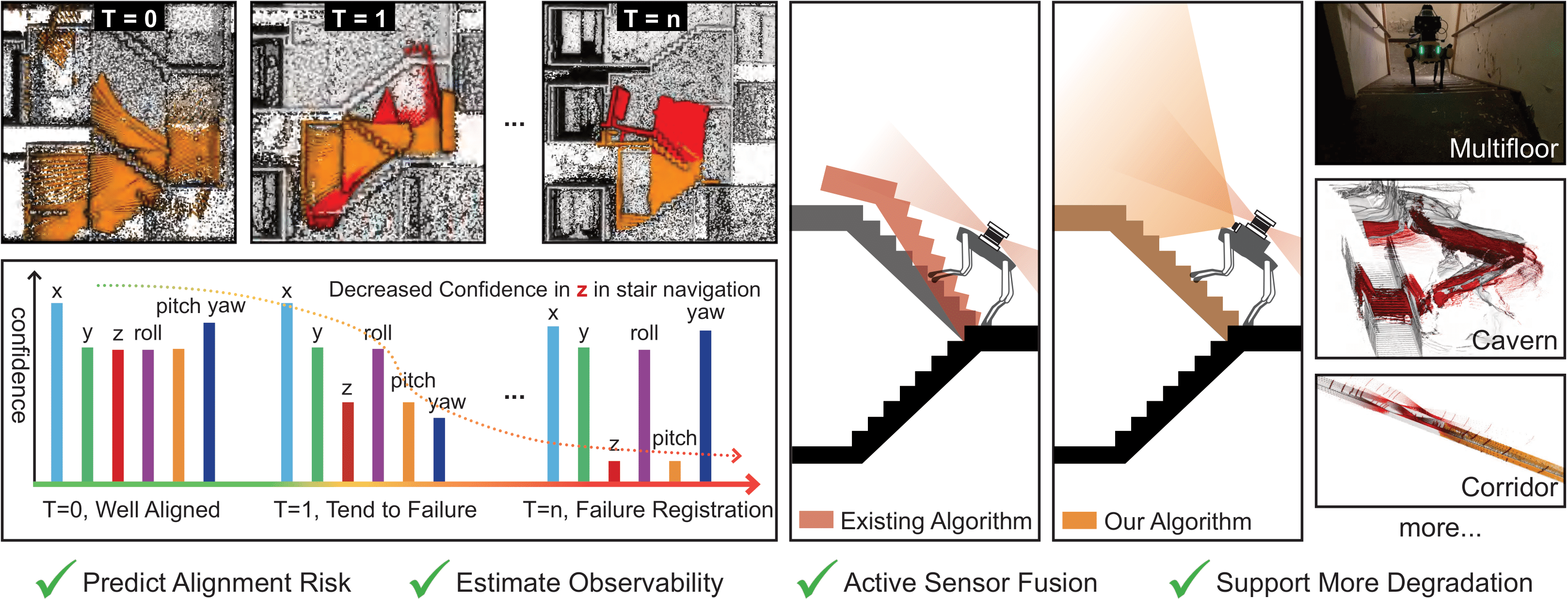
Dealing degeneracy with LiDAR-Inertial localization in SLAM (Simultaneous localization and mapping) community has been an active research topic for more than a decade. The motivation behind such research is to investigate failures in ICP (Iterative Closest Point), the principal algorithm used for LiDAR-Inertial localization. ICP calculates the optimal transformation between two sets of point clouds. As Censi[1] concluded, ICP failures occur due to three main reasons:
- Bad initial guess for ICP optimization
- Sensor Noise
- Degeneracy
To address the question Why Predict Alignment Risk?, we examine common approaches to detecting and preventing degeneracy in robotics and their limitations. Approaches from previous literature can be best categorized into two methods:
- Detect ICP failures under degeneracy through ICP hessian analysis[2][4][5] and use this analysis to constrain ICP pose solving.
- Fuse external sensor sources using pre-defined or ICP covariance[8] to prevent failures.
However, there are two limitations associate with using ICP hessian analysis and covariance-based sensor fusion:
- Degeneracy detection using ICP hessian is difficult to generalize across different sensor modalities and environments.
- Covariance under degeneracy is non-Gaussian.
This article will unfold these limitations in more details. But first, let's revisit how can we obtain ICP covariance and its hessian to detect degeneracy, using Prakhya et al.[4] and Tuna et al.[3] as reference.
ICP Covariance Modeling and Hessian Analysis
Let assume z be the measurements and x be the output of an function A that minimizes an objective function J i.e.,
\[\mathbf{x}=A(\mathbf{z})=\operatorname{argmin}_{\mathbf{X}} J(\mathbf{z}, \mathbf{x}) \tag{1}\]
Then the approximate value of the covariance of \(\mathbf{x}\) in terms of \(A(\mathbf{z})\) will be,
\[\operatorname{cov}(\mathbf{x})=\operatorname{cov}\left(\left.A(\mathbf{z})\right|_{\mathbf{z}=\mathbf{z}_o}\right) \approx \frac{\partial A}{\partial \mathbf{z}_o} \operatorname{cov}(\mathbf{z}) \frac{\partial A^T}{\partial \mathbf{z}_o}\tag{2}\]
Using the implicit function theorem:
\[\frac{\partial A}{\partial \mathbf{z}_o}=-\left(\frac{\partial^2 J}{\partial \mathbf{x}^2}\right)^{-1}\left(\frac{\partial^2 J}{\partial \mathbf{z} \partial \mathbf{x}}\right)\tag{3}\]
Rewrite the equation into:
\[\operatorname{cov}(\mathbf{x})=\left(\frac{\partial^2 J}{\partial \mathbf{x}^2}\right)^{-1}\left(\frac{\partial^2 J}{\partial \mathbf{z} \partial \mathbf{x}}\right) \operatorname{cov}(\mathbf{z})\left(\frac{\partial^2 J}{\partial \mathbf{z} \partial \mathbf{x}}\right)^T\left(\frac{\partial^2 J}{\partial \mathbf{x}^2}\right)^{-1}\tag{4}\]
The objective function for point-to-point ICP is formulated as:
\[J=\sum_{i=1}^n\left\|\mathbf{R} \mathbf{P}_{\mathbf{i}}+\mathbf{T}-\mathbf{Q}_{\mathbf{i}}\right\|^{\mathbf{2}}\tag{5}\]
where \(\{\mathbf{P}_{\mathbf{i}},\mathbf{Q}_{\mathbf{i}}\}\) are the point cloud correspondences, and \([\mathbf{R}, \mathbf{T}]\) is the homogeneous transformation estimated by ICP. The ICP covariance can be calculated using the above equation, where \(\mathbf{x}=\left[\begin{array}{@{}llllll@{}}x & y & z & r & p & y\end{array}\right]\) and \(\mathbf{z}\) represents \(n\) sets of correspondences \(\{\mathbf{P}_{\mathbf{i}},\mathbf{Q}_{\mathbf{i}}\}\). \(\frac{\partial^2 \mathbf{J}}{\partial \mathbf{x}^2}\) is the ICP hessian matrix \(\mathbf{H} \in \mathbb{R}^{6\times6}\).
Apply eigen-decomposition to \(\mathbf{H}\):
\[\boldsymbol{H}=\boldsymbol{V} \Sigma \boldsymbol{V}\tag{6}\]
where diagonal element of \(\Sigma \in\left\{\operatorname{diag}(\boldsymbol{v}): \boldsymbol{v} \in \mathbb{R}_{\geq 0}^n\right\}\) are eigenvalues and \(\boldsymbol{V} \in \mathbb{R}^{6 \times 6}\) are the eigenvectors in matrix form. The idea of degeneracy detection is to observe the null space of \(\mathbf{H}\). By examining \(\Sigma\), one can identify the least-constrained pose elements of \(\mathbf{x}\) by looking at the lowest eigenvalues.
Degeneracy detection using ICP hessian is difficult to generalize
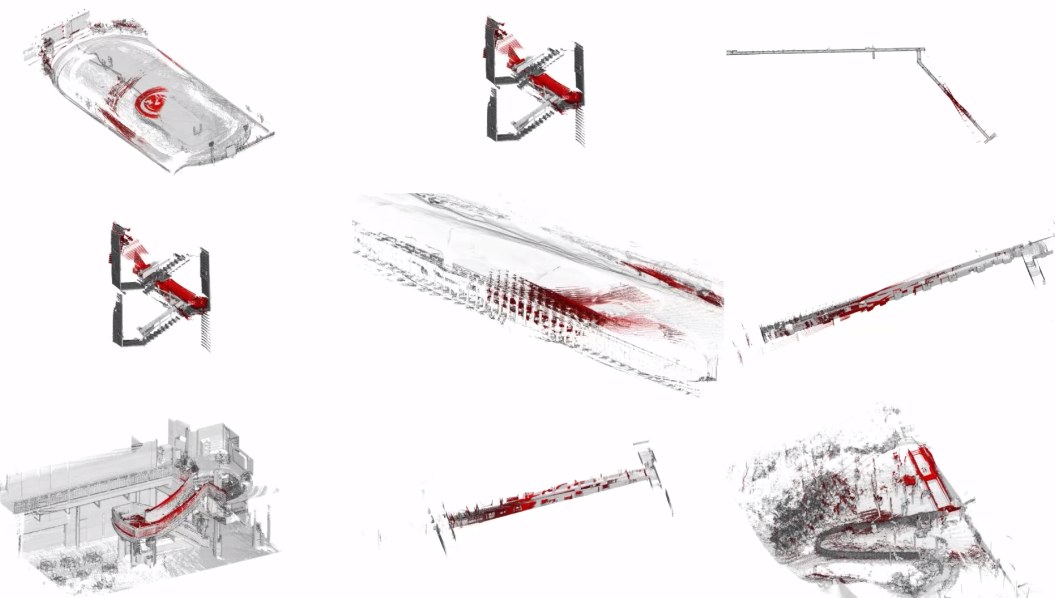
The effectiveness of ICP hessian analysis for degeneracy detection varies significantly across different LiDAR sensors and environments. Nubert et al. [6] demonstrated this variability through an experiment comparing the lowest eigenvalues from two LiDAR sensors: Velodyne and Ouster, as shown in Fig. 1. Additional validation using the SuperLoc dataset (Cave03 and Floor01) revealed similar variations across different environments, as shown in Fig. 2. These large differences in lowest eigenvalues indicate that eigenvalue-based parameters cannot be over-applied across different sensor modalities or environments, limiting the Hessian's generalizability. This makes constrained ICP using eigenvalue-based appraoch [5][6] less durable.
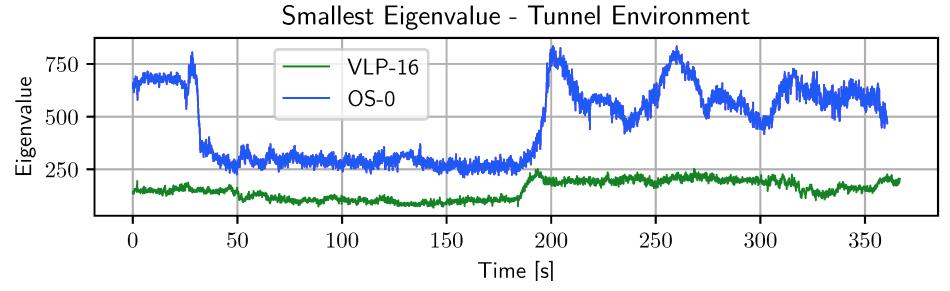
Figure 1: Comparison between different LiDAR sensors (Nubert et al.)
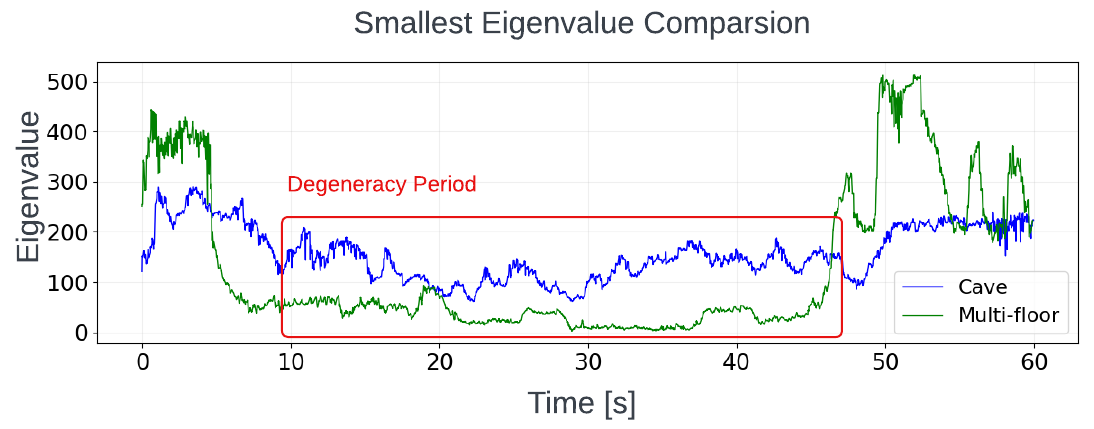
Figure 2: Comparison between different environments: Degeneracy period indicates the most degraded section of each dataset.
Covariance under degeneracy is non-Gaussian
A Gaussian noise model is crucial for performing sensor fusion. As mentioned earlier, sensor fusion with external sources such as visual odometry, GPS, etc. is a common method to prevent degeneracy. Sensor fusion is typically implemented using either Factor Graphs (GTSAM)[7] or Extended Kalman Filters (EKF). Both approaches solve for pose estimates based on the assumption that all sensor measurements follow a Gaussian noise model. In other words, the covariance matrix for each measurement needs to be non-singular or full rank. In SuperLoc, we use Factor Graphs, which inference Maximum a Posteriori (MAP) estimation with Gaussian noise models into a nonlinear least-squares problem.
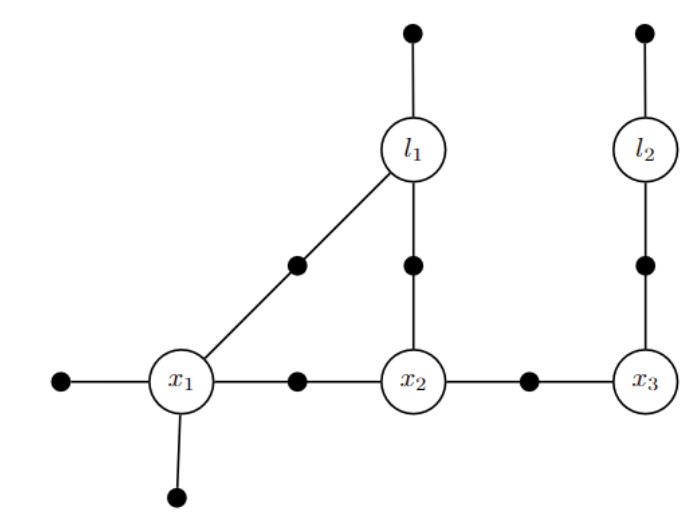
Figure 3: Factor graph for the toy SLAM problem
\[X^{\text {MAP }} =\underset{X}{\operatorname{argmax}} \phi(X) =\underset{X}{\operatorname{argmax}} \prod_i \phi_i\left(X_i\right)\tag{7}\]
Here, \(\phi_i\left(X_i\right)\) are factors, represented by black dot in Fig. 3. Each factor is a function of state variable \(x_i\) and measurement \(z_i\). \(h_i\) is the measurement function that remap state variable \(x_i\) into measurement space.
\[\phi_i\left(X_i\right) \propto \exp \left\{-\frac{1}{2}\left\|h_i\left(X_i\right)-z_i\right\|_{\Sigma_i}^2\right\}\tag{8}\]
Take negative log of \(\underset{X}{\operatorname{argmax}}\) of Eq. 6, and drop \(\frac{1}{2}\) factor,
\[X^{\text {MAP }}=\underset{X}{\operatorname{argmin}} \sum_i\left\|h_i\left(X_i\right)-z_i\right\|_{\Sigma_i}^2\tag{9}\]
Rewrite the Mahalanobis norm as some term e:
\[\|e\|_{\Sigma}^2 \triangleq e^{\top} \Sigma^{-1} e=\left(\Sigma^{-1 / 2} e\right)^{\top}\left(\Sigma^{-1 / 2} e\right)=\left\|\Sigma^{-1 / 2} e\right\|_2^2\tag{10}\]
And with linearization of nonlinear problem,
\[h_i\left(X_i\right)=h_i\left(X_i^0+\Delta_i\right) \approx h_i\left(X_i^0\right)+H_i \Delta_i\tag{11}\]
where Jacobian \(H_i\) is \(\frac{\partial h_i\left(X_i\right)}{\partial X_i}\), and we can rewrite Eq. 9 into,
\[\begin{aligned}
\Delta^* & =\underset{\Delta}{\operatorname{argmin}} \sum_i\left\|h_i\left(X_i^0\right)+H_i \Delta_i-z_i\right\|_{\Sigma_i}^2 \\
& =\underset{\Delta}{\operatorname{argmin}} \sum_i\left\|H_i \Delta_i-\left\{z_i-h_i\left(X_i^0\right)\right\}\right\|_{\Sigma_i}^2
\end{aligned}\tag{12}\]
Pre-multiply Jacobian \(H_i\) and prediction error by \(\Sigma^{-1 / 2}\) using Eq. 10,
\[\begin{aligned}
A_i & =\Sigma_i^{-1 / 2} H_i \\
b_i & =\Sigma_i^{-1 / 2}\left(z_i-h_i\left(X_i^0\right)\right)
\end{aligned}\tag{13}\]
The final standard least-squares problem,
\[\begin{aligned}
\Delta^* & =\underset{\Delta}{\operatorname{argmin}} \sum_i\left\|A_i \Delta_i-b_i\right\|_2^2 \\
& =\underset{\Delta}{\operatorname{argmin}}\|A \Delta-b\|_2^2
\end{aligned}\tag{14}\]
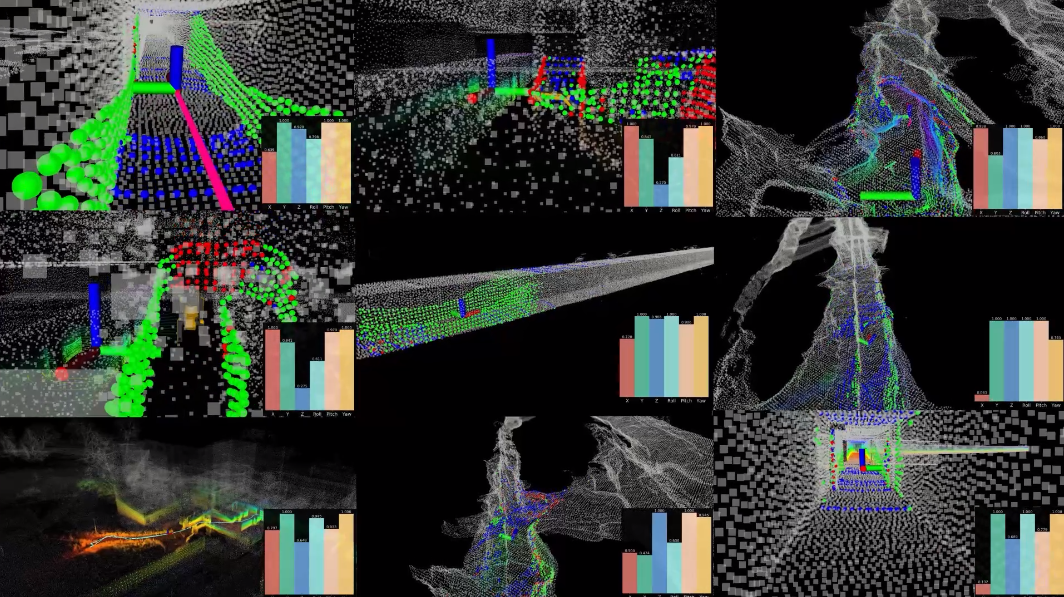
To calculate Equation 10, one can either use a pre-defined covariance or ICP covariance. However, this covariance becomes non-Gaussian or rank-deficient under degeneracy. Our cave dataset demonstrates this through high condition numbers in the ICP covariance matrix just before localization failures, as shown in Fig. 4. This indicates imminent rank deficiency during degeneracy. Using rank-deficient covariance in factor graph optimization results in unconstrained pose estimates along the degenerate direction, as shown in Fig. 5. Therefore, maintaining a well-ranked ICP covariance is crucial for optimal sensor fusion.
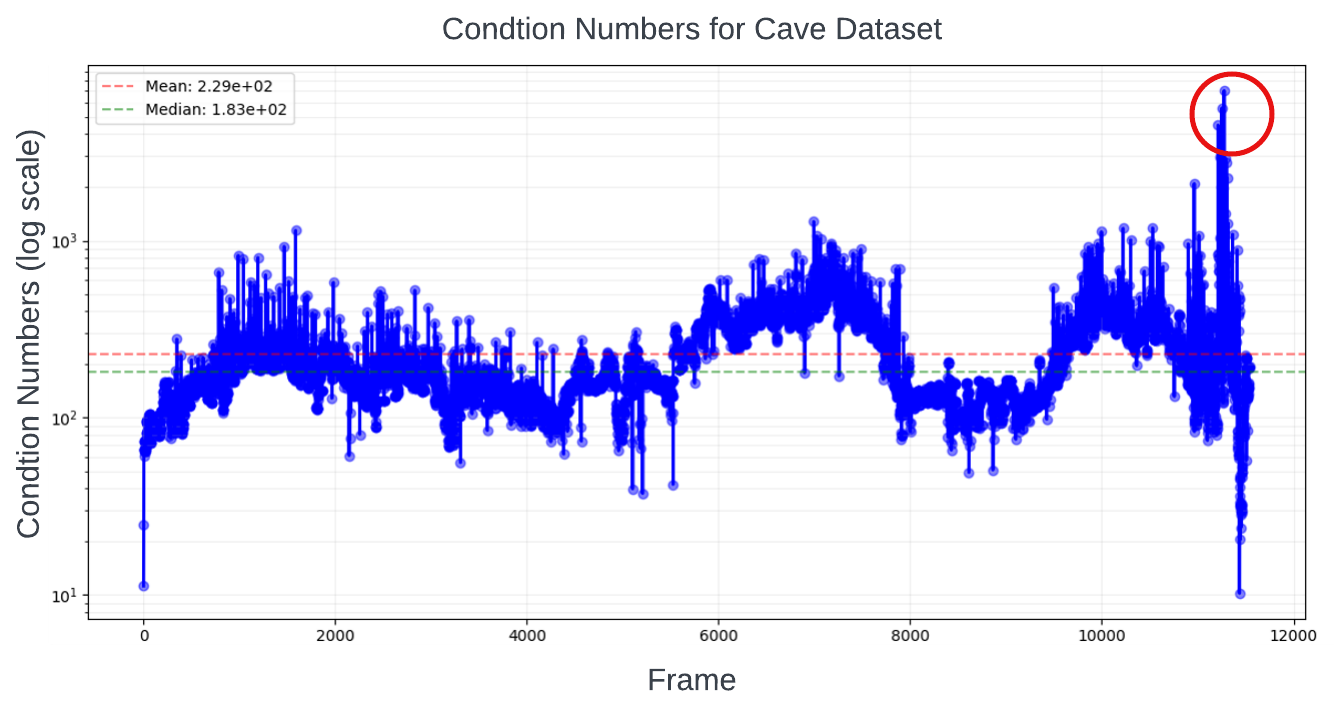
Figure 4: Large conditional number is present when degeneracy happened
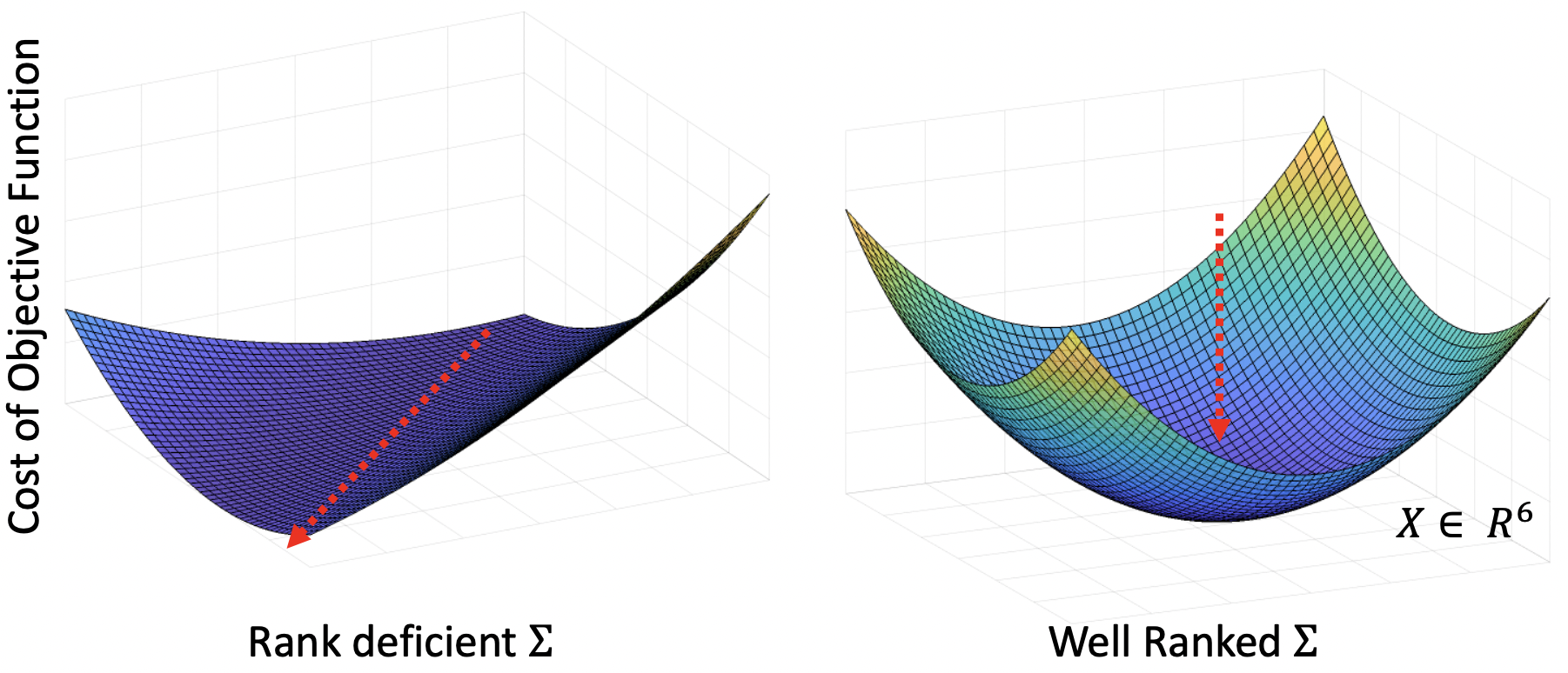
Figure 5: Visual representation of factor graph objective function: The red arrow indicates an unconstrained direction in the solution space for rank-deficient cases.
Conclusion
We have examined key limitations in using ICP hessian its covariance for degeneracy detection and prevention in LiDAR-inertial localization. First, we demonstrated that eigenvalue-based degeneracy detection lacks generalizability across different sensor modalities and environments, as evidenced by significantly varying eigenvalue patterns between different LiDAR sensors and testing environments. Second, we showed that ICP covariance becomes non-Gaussian under degeneracy, leading to unconstrained solutions in factor graph optimization. For our Predict Alignment Risk, we first detect degeneracy at front end rather then during ICP. Our method analyzes the geometric contribution of pointcloud features and quantify a scale between [0, 1], making it more applicable to different cases compared to eigenvalues. Next, we use this risk to formulate full rank covariance to allow sensor fusion with other sensors using our Active Sensor Fusion. This makes our Predict Alignment Risk more robust and reliable compare to ICP analysis approach.
References
A. Censi, "An accurate closed-form estimate of icp's covariance", in Proceedings 2007 IEEE international conference on robotics and automation
J. Zhang, M. Kaess, and S. Singh, "On degeneracy of optimization-based state estimation problems", in 2016 IEEE International Conference on Robotics and Automation (ICRA)
S. M. Prakhya, L. Bingbing, Y. Rui and W. Lin, "A closed-form estimate of 3D ICP covariance", 2015 14th IAPR International Conference on Machine Vision Applications (MVA), Tokyo, Japan
Tuna, T., Nubert, J., Nava, Y., Khattak, S., & Hutter, M. (2022). "X-ICP: Localizability-Aware LiDAR Registration for Robust Localization in Extreme Environments", arXiv preprint arXiv:2211.16335
W. Talbot et al., "Principled ICP Covariance Modelling in Perceptually Degraded Environments for the EELS Mission Concept," 2023 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Detroit, MI, USA
J. Nubert, E. Walther, S. Khattak and M. Hutter, "Learning-based Localizability Estimation for Robust LiDAR Localization," 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 2022
M. Kaess, H. Johannsson, R. Roberts, V. Ila, J. Leonard and F. Dellaert, "iSAM2: Incremental smoothing and mapping with fluid relinearization and incremental variable reordering," 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 2011
W. Xu and F. Zhang, "FAST-LIO: A Fast, Robust LiDAR-Inertial Odometry Package by Tightly-Coupled Iterated Kalman Filter," in IEEE Robotics and Automation Letters, vol. 6, no. 2, pp. 3317-3324, April 2021
 arXiv
Code
Robustness Metrics
arXiv
Code
Robustness Metrics